Introduction
Sliding Window Technique is one of the common dynamic programming techniques, frequently used to optimize algorithms that involve searching an array or string for a consecutive subsection that satisfies a given condition by reducing its time complexity, most of the time by replacing a nested loop algorithm with a single loop. Let's see this in practice.
Brute Force Approach
Problem : given an array of integers 'arr', calculate the maximum sum of 'k' consecutive elements in the array.
We start with first index and sum till k-th element. We do it for all possible consecutive blocks or groups of k elements. This method requires nested for loop, the outer for loop starts with the starting element of the block of k elements and the inner or the nested loop will add up till the k-th element.
let maxSumBruteForce = (arr, k) => {
if (k > arr.length) {
return null;
}
let maxSum = -Infinity;
for (let i = 0; i < arr.length - k + 1; i++) {
let currentSum = 0;
for (let j = 0; j < k; j++) {
currentSum += arr[i + j];
}
maxSum = Math.max(maxSum, currentSum);
}
return maxSum;
};
Input : arr = [1, 4, 2, 10, 2, 3, 1, 0, 20] , k = 4
output : 24
time complexity is O(n*k) , as we notice from the above code that the outer loop is going through n - k + 1 item, but when n is much larger than k, we can forget about the k + 1 part we can just call it n items, and the inner loop is going through k items so we have O(n*k) .
Can we optimize this solution and get the BigO down to O(n) ?
yes, that's where the sliding window pattern comes into play.
Fixed-Size Sliding Window Approach
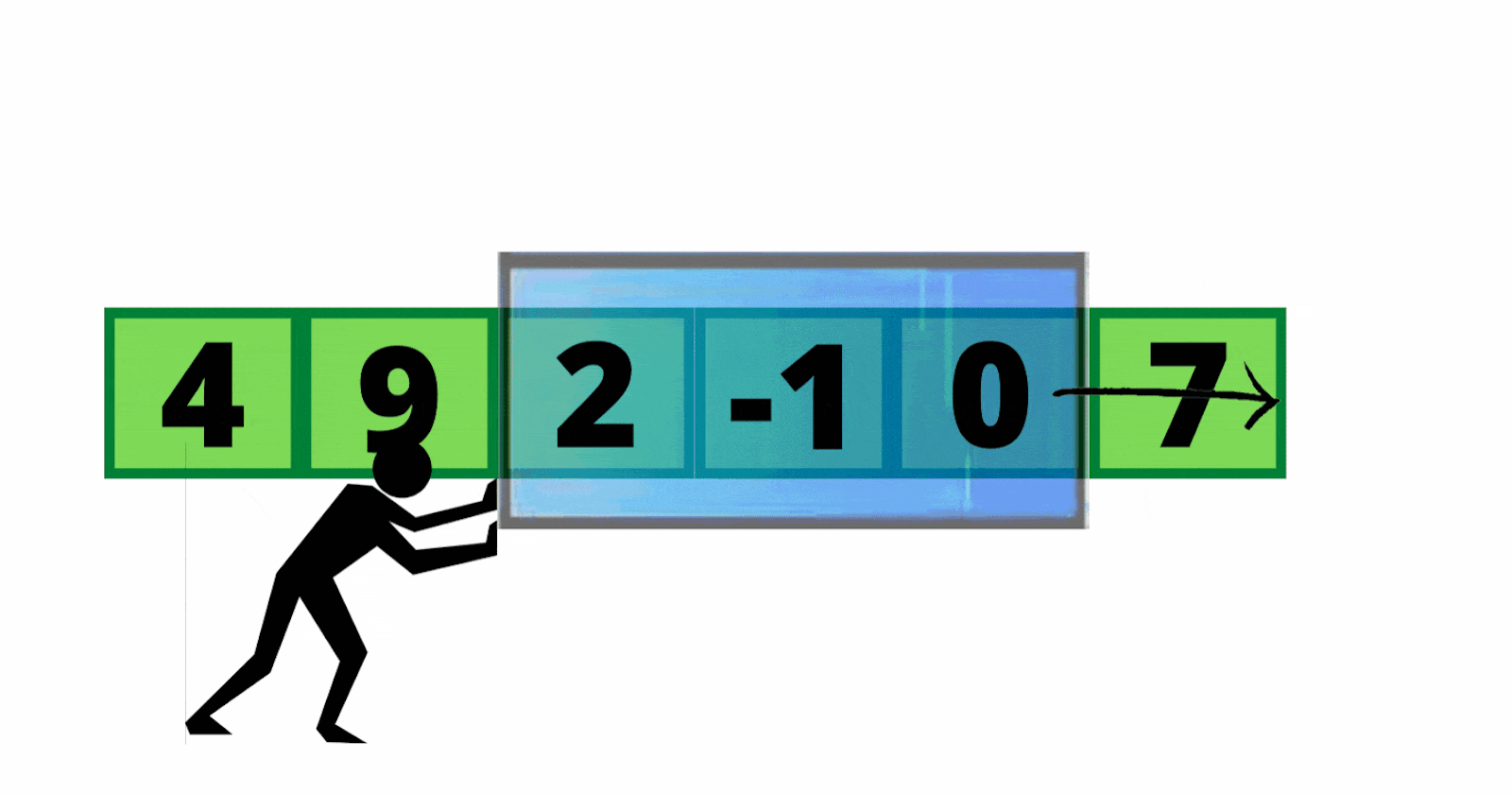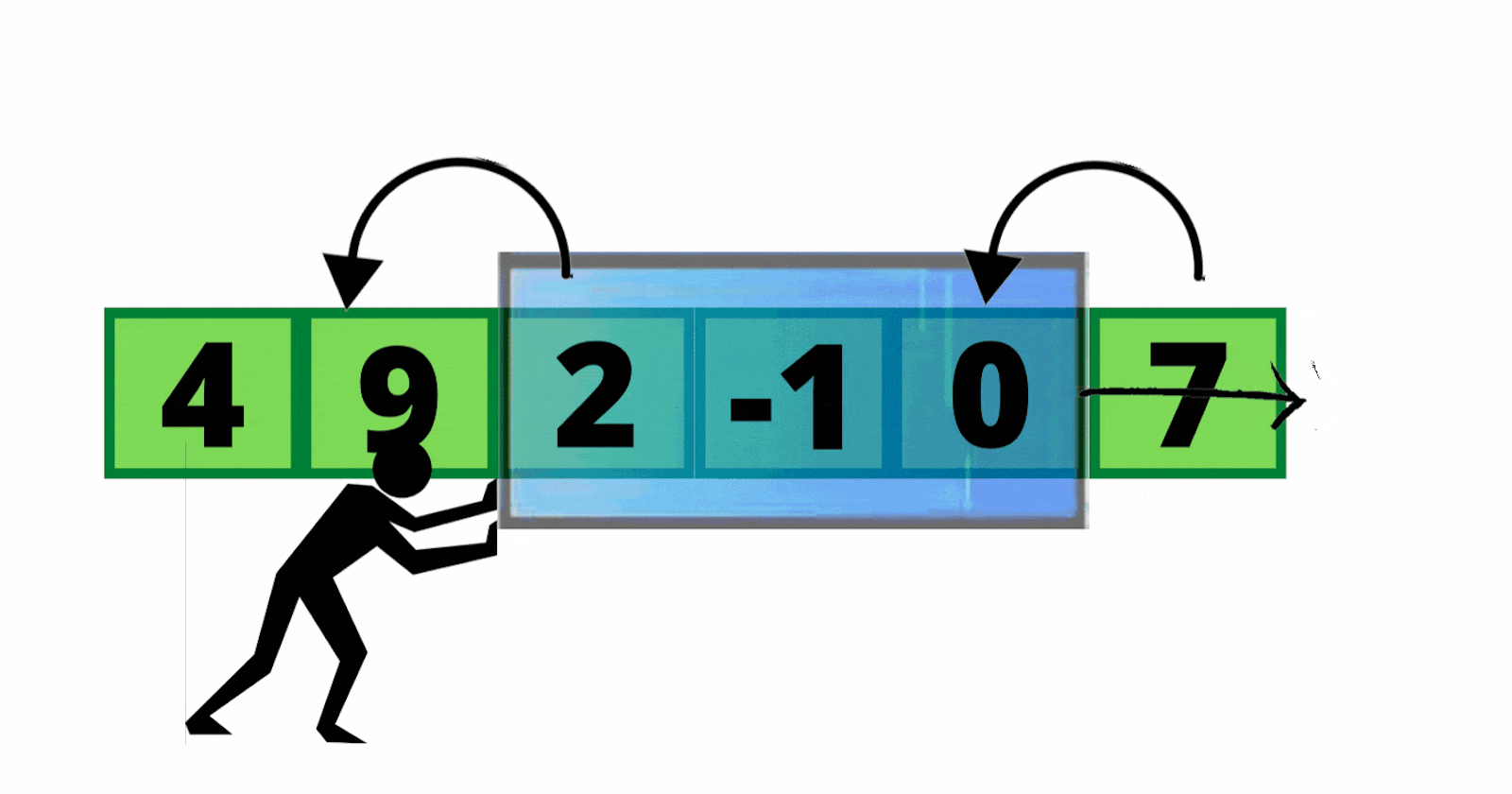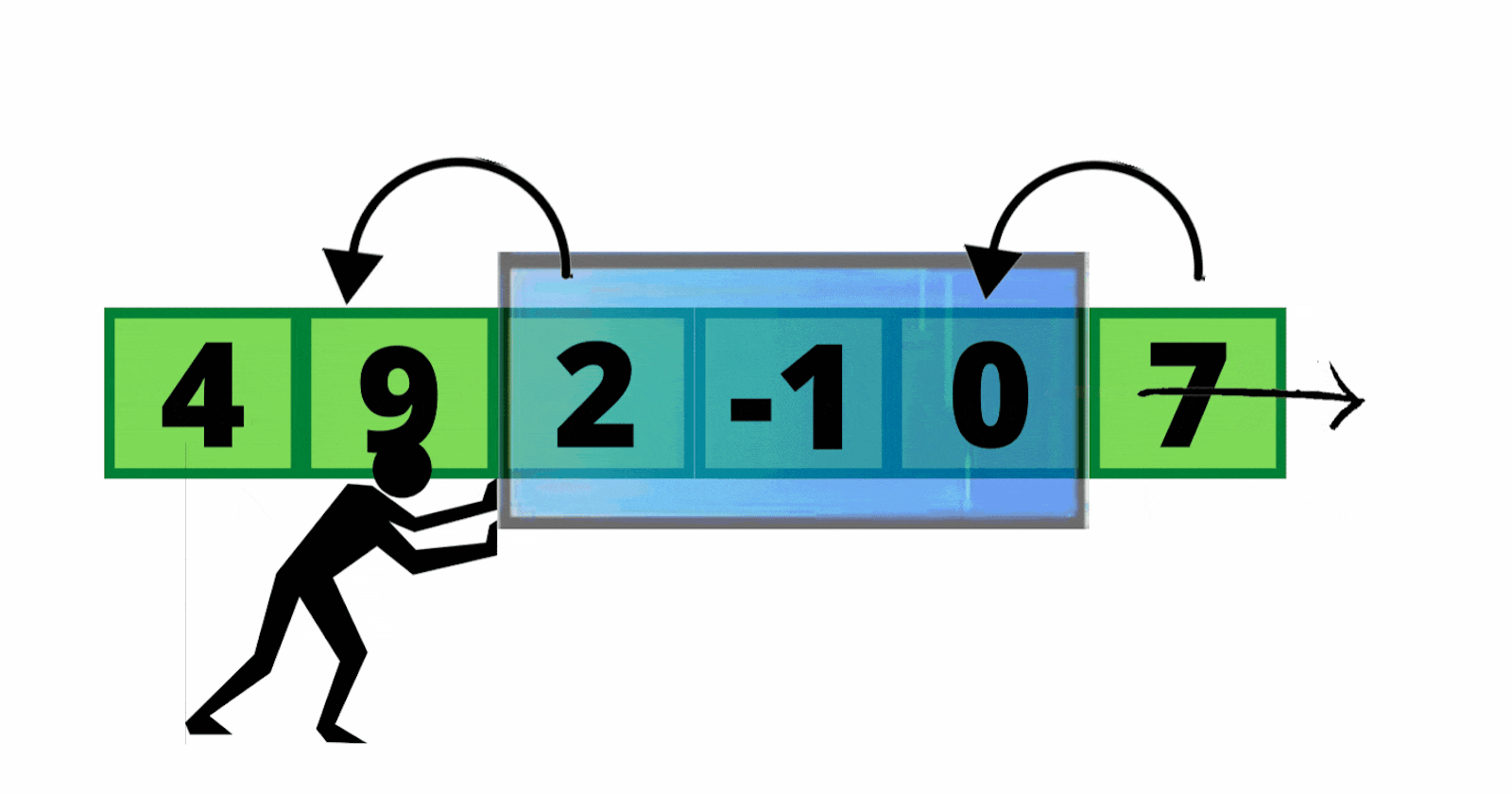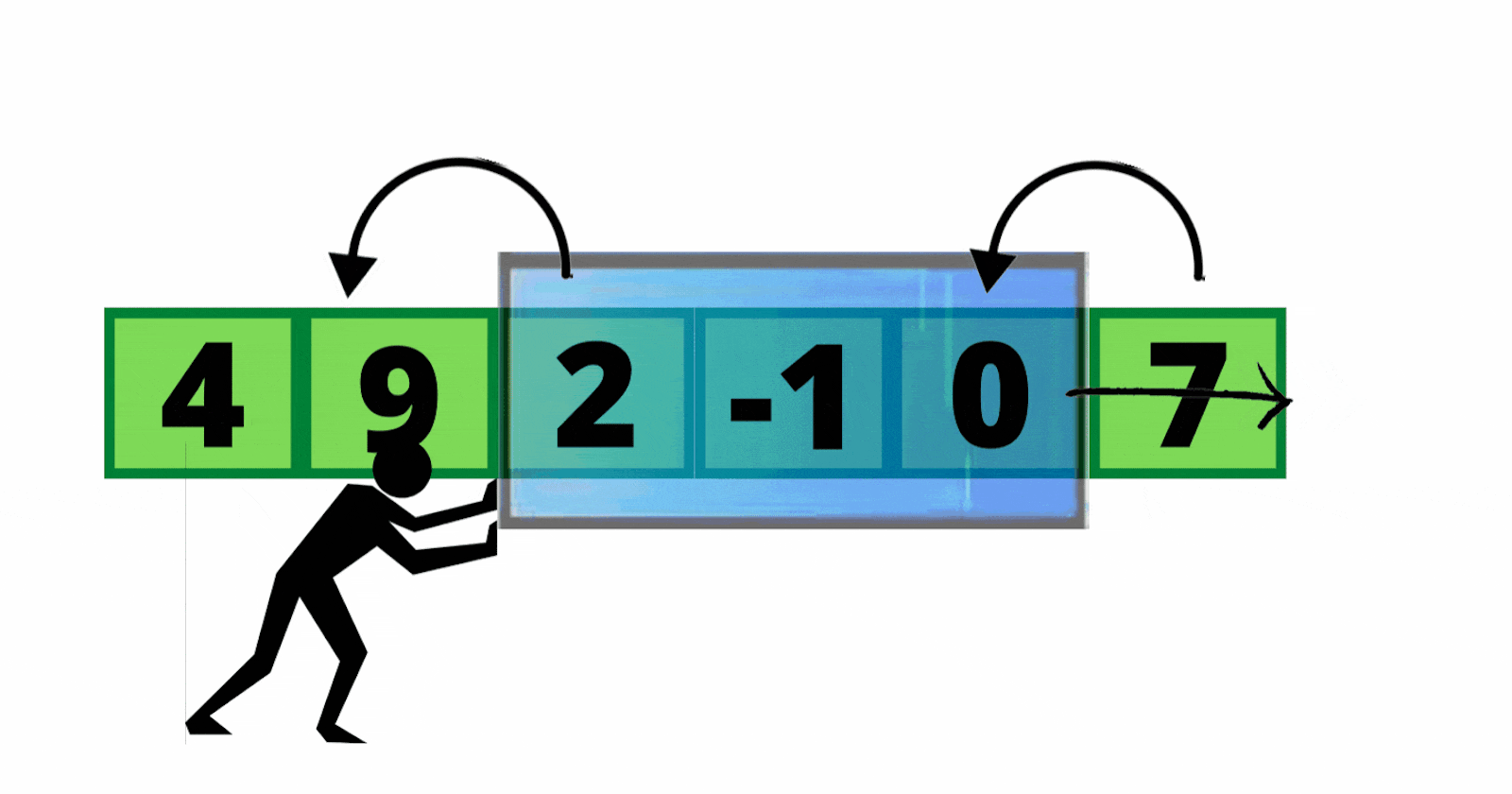
The below representation clearly explains how the sliding window works :
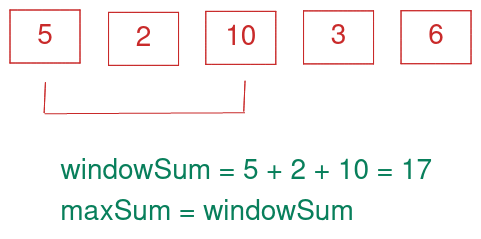
given the array arr = [5, 2, 10, 3, 6] and k = 3
- In the initial phase, imagine two pointers that represent the current subsection (window) of the array. one pointer is the leading edge and the other is the trailing edge. this window represents the first k elements of the array. we compute the sum of this window elements using a linear loop and store the sum in windowSum variable, then set the maxSum to the initial windowSum value which is 17.
- Then, we slide our window by a unit index. meaning that we add the next element 3 in this case and subtract the first element of the previous window 5 in this case, so our windowSum becomes 15. Now, we compare this windowSum with the maxSum. since it's smaller, we won't change the maxSum value.

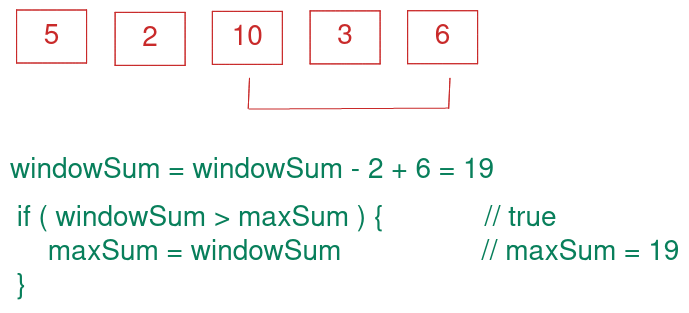
- Again, we slide our window by a unit index by adding 6 and subtracting 2. the new windowSum will be 19. again we compare this value with maxSum which is 17, and because it's greater, we will set it as our new maxSum.
The following code is the implementation for the above approach :
let maxSumSlidingWindow = (list, k) => {
if (k > list.length) {
return null;
}
let maxSum = 0;
let windowSum = 0;
for (let i = 0; i < k; i++) {
windowSum += list[i];
}
maxSum = windowSum;
for (let i = k; i < list.length; i++) {
windowSum -= list[i - k] + list[i];
maxSum = Math.max(maxSum, windowSum);
}
return maxSum;
};
As you can see now,
Time Complexity is O(n).
Dynamic-Size Sliding Window Approach
Let's go one step further and make the window size dynamic rather than being fixed.
The idea here is that the window grows (by incrementing the leading edge) or shrinks (by incrementing the trailing edge), moving it along the data structure.
The window keeps inching along until it reaches the stopping condition, usually the end of the data structure.
Problem : given an array of positive integers 'arr', and a positive integer 'num'. write a function that should return the minimal length of a contiguous subarray of which the sum is greater than or equal to the integer 'num'. if there isn't return 0.
- Input: arr = [2,1,6,5,4] , num = 9
- Output: 2
The below representation shows how the window being resized on each iteration :

The following code is the implementation for the previous approach :
function minSubArrayLen(arr, num) {
// to check sum of values against num
let sum = 0
// to track window's leading edge
let right = 0
// to track window's trailing edge
let left = 0
// to track smallest subarray length
let minLen = Infinity
// while window's trailing edge has NOT reached the end of the array
while (left < arr.length) {
// if window's leading edge has NOT reached the end of the array
// AND window's values do NOT add up to num, grow window to right
if(right < arr.length && sum < num) {
// increase sum by the value at window's leading edge
sum += arr[right]
// increment window's leading edge to grow window
right++
} else if(sum >= num){
// if window's values DO add up to AT LEAST num, shrink window from left
// update smallest subarray length to the lesser of current minLen or window's length
minLen = Math.min(minLen, right - left)
// decrease sum by the value at window's trailing edge
sum -= arr[left]
// increment window's trailing edge to shrink window
left++
} else {
// current sum is less than num, BUT window's leading edge HAS reached end of array
// needed to prevent an infinite loop
break
}
}
// return smallest subarray length found or 0
// if minLen is never updated, then there is NOT a sum >= num, so return 0
return minLen === Infinity ? 0 : minLen
}